On PERT

Estimating projects in software development. You're a manager or a team lead. You have some tasks, tens or hundreds of them. You need to know the duration and cost of the project consisting of these tasks. At least you need the estimation in man-hours (yeah, mythical). Let's skip here another magic of converting man-hours into calendar months and budget.

How do you get the man-hours for the project? You ask developers. How many hours do they need to implement each task? Then you sum these hours. Is this estimate reliable? Can you use this sum to request a budget? No.

Obviously you need to ask yourself how many hours you need to manage this project. And ask devops how many hours they will need to deploy it and set up CI/CD pipelines. And ask testers how many hours they will need to test each of the tasks. Just add more tasks not directly related to development but which require additional effort.

Can you trust the numbers now? Not yet.

The hours provided by the developers are only mean values of some random variables. Each task can be done faster, if you're lucky. Or slower, in case of any problems. Unfortunately, developers typically are too optimistic, they don't like to think about possible problems. And you, as a manager, need to compensate for this overly optimistic estimate.

The simplest approach is to multiply the original estimations. By two. Or by three. Or by pi. Depending on how experienced your developers are in estimating.

There's even a humorous explanation why the multiplier should be π + 1 (for the experienced team): the Bobuk-Bacek method.

You can do something smarter. You may add one more number, in addition to the mean man-hours, for each task. A measurement of your (and the team's) uncertainty in this estimation. It can be a contingency percentage, a buffer to add for the case if something goes wrong. 30% – 50% – 150% – ... You may guess anything.

Anyway you add buffers. To be spent according to Parkinson's law.

Are there better ways to identify the uncertainty than just guessing? Yes. PERT.

PERT stands for Program Evaluation and Review Technique. It was originally developed for the US Navy in 1958. In 1958, Carl! PERT is commonly used together with Critical Path Method (CPM), which is more known than PERT. CPM is used mostly to convert estimates into calendar schedules. While PERT is to calculate the estimations.

Well... My wife asks me to wash clothes on the weekend. As an experienced manager I want to know how much time it may take. As I also have other plans for the weekend.

I know that it's necessary to take clothes from the laundry basket, put them in the washing machine, add some powder, select the Normal program, and press Start button. And it should wash for about 90 minutes. Round it up to 2 hours.

This is the only number which is typically provided by developers. But we want to do it in a PERT way. So, name the initial number as Most likely. And switch to optimist mode first.

What's the best thing that can happen with the clothes washing? I look at the laundry basket and see no clothes to wash, or just a pair of socks there. Cool! No need to wash today. So, I'm setting the optimistic estimation to zero, which means there can be no need to do this task at all. Ok, actually it's not zero, it takes 20 seconds to go to the laundry and check the basket. Just round it to zero.

Next step. Switch to pessimist mode. I need to find out how long it can take if anything goes wrong.

What can be wrong? I may discover the washing powder is over, so I have to drive to a supermarket and buy some. +1 hour. I may have found a wool sweater in the basket. I'm an experienced developer, so I know that wool clothes must be washed separately, using a special Delicate program. And this program is typically longer. +2 hours. So, I hope the weekend washing will not take more than 5 hours.

More importantly, it doesn't make sense (for me) to spend more than 5 hours on washing. If it's going to take more than 5 hours, I should cancel this activity and reschedule my weekend. Maybe I should schedule two days for washing. Anyway, I need to review all the tasks and update the estimation.

Okay, I have three numbers: optimistic, most likely, and pessimistic estimates. Now it's time to use PERT.

The expected hours for each task are the weighted average, where the most likely has the weight of four.

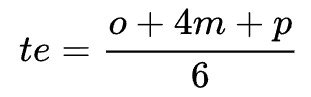
It can be easily calculated in any spreadsheet.

The sum of the expected time for the whole project is a common arithmetical sum of the expected time of each task.

Okay. I know that clothes washing should take 2.2 hours. And definitely no more than 5 hours. In many cases this knowledge is enough.

But PERT also allows you to find the standard deviation. It's a difference between optimistic and pessimistic estimates, divided by six.

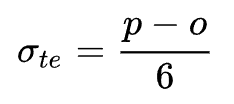
Again, easy to calculate in a spreadsheet.

Finding the total SD for the whole project by combining the SDs of all tasks is a bit tricky. You need to sum squares and take the square root of it.

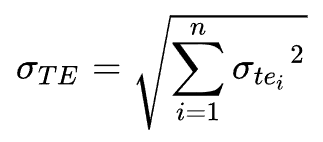
Now, with standard deviation, you can find the confidence interval for the random variable of your project length.

According to Wikipedia:

• The 68% confidence interval for the true project work time is approximately E(project) ± SD(project)
• The 90% confidence interval for the true project work time is approximately E(project) ± 1.645 × SD(project)
• The 95% confidence interval for the true project work time is approximately E(project) ± 2 × SD(project)
• The 99.7% confidence interval for the true project work time is approximately E(project) ± 3 × SD(project)
• Information Systems typically uses the 95% confidence interval for all project and task estimates.

So, for my washing project, I finally get 2.2 ± 1.7 hours with 95% confidence.

All this magic works because PERT has its own PERT distribution. By providing these three numbers, optimistic, most likely, pessimistic estimates, you define a random variable. If your most likely estimate falls exactly in the middle between optimistic and pessimistic values, you get a symmetric normal distribution. If you're not certain about the task, you should declare a large enough pessimistic value. You don't need infinity, but you should define a point where to stop to re-think, update your plan, and re-estimate. In this case the PERT distribution will have a long tail, stating your uncertainty.

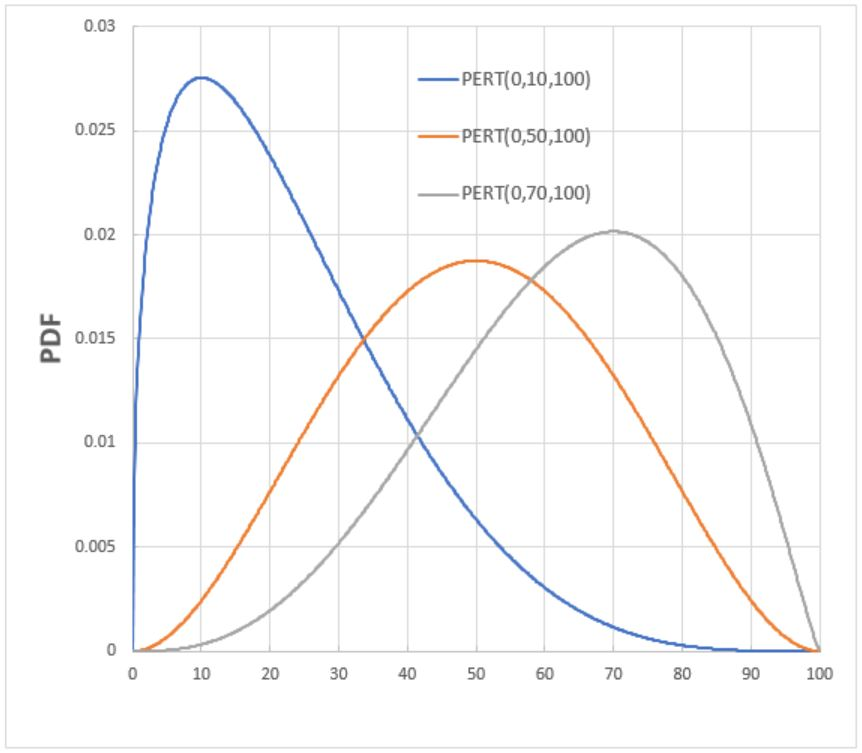
So, asking developers for not only one, but for three numbers, you can involve some maths invented in 1958 to get precise estimation declaring your uncertainty and confidence interval. But also you force the developers (and other team members) to think not only optimistically, but also pessimistically. To think about risks. This is PERT estimation.

Wikipedia articles:

• Program evaluation and review technique
• PERT distribution
• Three-point estimation